\( \DeclareMathOperator{\abs}{abs}
\newcommand{\ensuremath}[1]{\mbox{$#1$}}
\)
\[\mbox{}\\\mbox{0 errors, 0 warnings}\]
\[\tag{%o14} /usr/local/share/maxima/5.41.0/share/draw/draw.lisp\]
\[\tag{line}[[-2,-3],[-1,-\frac{1}{2}],[0,0],[1,2],[2,3]]\]
\[\tag{%o60} \operatorname{polyL}\left( \mathit{liste}\right) :=\]
\[\tag{%o61} \frac{\left( x-1\right) x\, \left( x+1\right) \, \left( x+2\right) }{8}-\frac{\left( x-2\right) x\, \left( x+1\right) \, \left( x+2\right) }{3}+\frac{\left( x-2\right) \, \left( x-1\right) x\, \left( x+2\right) }{12}-\frac{\left( x-2\right) \, \left( x-1\right) x\, \left( x+1\right) }{8}\]
\[\tag{%o68} \operatorname{pl}(x):=\operatorname{polyL}\left( \mathit{line}\right) \]
\[\tag{%t69} \]
\newcommand{\ensuremath}[1]{\mbox{$#1$}}
\)
(%i14) | load(draw); |
\[\mbox{}\\\mbox{0 errors, 0 warnings}\]
\[\tag{%o14} /usr/local/share/maxima/5.41.0/share/draw/draw.lisp\]
(%i15) | line : [[−2,−3], [−1, −1/2], [0,0], [1, 2], [2,3]]; |
\[\tag{line}[[-2,-3],[-1,-\frac{1}{2}],[0,0],[1,2],[2,3]]\]
(%i60) | polyL(liste) := block([i,n,polyComplet, polyLagrange, p, a], n : length(liste), polyComplet : product( x−liste[i][1], i, 1, n), polyLagrange : 0, for i from 1 thru n do ( p : polyComplet/(x − liste[i][1]), a : subst(liste[i][1], x, p), polyLagrange : polyLagrange + liste[i][2]·p/a ), polyLagrange ); |
\[\tag{%o60} \operatorname{polyL}\left( \mathit{liste}\right) :=\]
(%i61) | polyL(line); |
\[\tag{%o61} \frac{\left( x-1\right) x\, \left( x+1\right) \, \left( x+2\right) }{8}-\frac{\left( x-2\right) x\, \left( x+1\right) \, \left( x+2\right) }{3}+\frac{\left( x-2\right) \, \left( x-1\right) x\, \left( x+2\right) }{12}-\frac{\left( x-2\right) \, \left( x-1\right) x\, \left( x+1\right) }{8}\]
(%i68) | pl(x) := polyL(line); |
\[\tag{%o68} \operatorname{pl}(x):=\operatorname{polyL}\left( \mathit{line}\right) \]
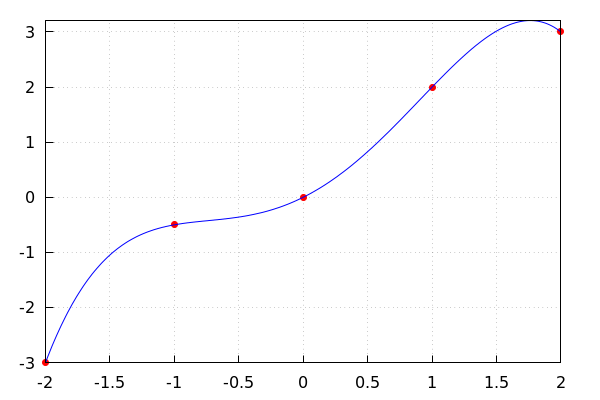
(%i69) | wxdraw2d( grid = true, point_type=7, color=red, points(line), color=blue, explicit(pl(x), x, −2, 2) ); |
\[\tag{%t69} \]

\[\tag{%o69} \]
