Théorème de Ferraris – champs tournants
Le théorème de Ferraris démontre qu’un champ tournant peut être créé par trois bobines positionnées en arc de cercle avec un décalage de 120°, chacune alimentées par une phase d’un courant électrique triphasé1. La fréquence de rotation est alors égale à la fréquence de courants d’alimentation. Il démontre également que 3p bobines alimentées en triphasé et décalées de 120°/p permettent d’obtenir un champ tournant avec une fréquence de rotation f/p, f étant la fréquence des courants d’alimentation.
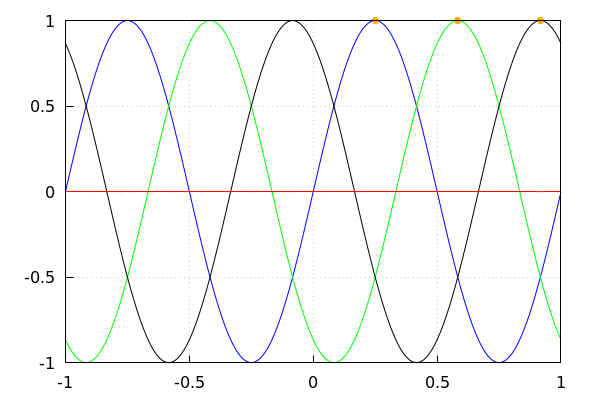
Définition de trois champs périodiques dans l’espace, période = D
champs B1, B2, B3 décalés de D/3
(%i3) |
B1(B, D, x) := B·sin(2·%pi·x/D) ; B2(B, D, x) := B·sin(2·%pi/D·(x − D/3)); B3(B, D, x) := B·sin(2·%pi/D·(x − 2·D/3)); |
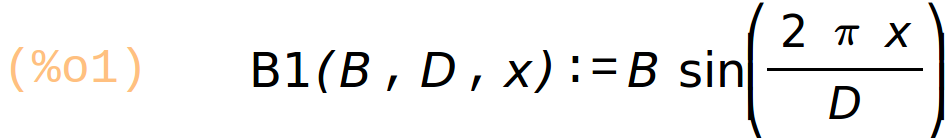
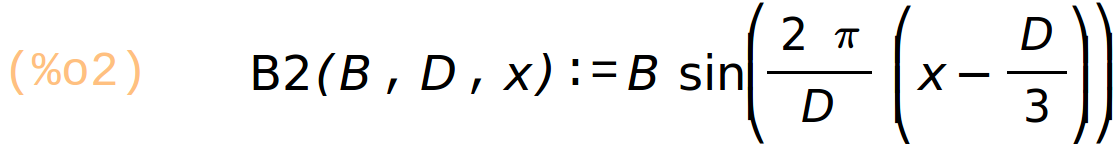
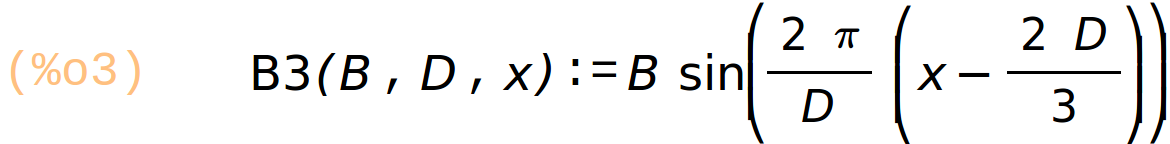
(%i4) |
sommeB(B, D, x) := B1(B,D,x) + B2(B,D,x) + B3(B,D,x); |
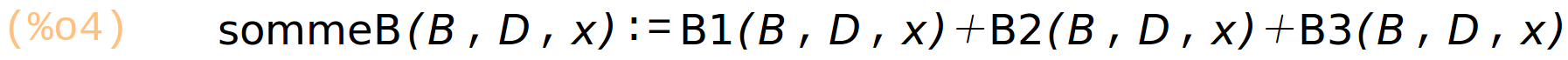
(%i6) |
f : 50; T: 1/f; |


(%i10) |
load(draw); D : 1; line : [[D/4, 1], [D/3+D/4, 1], [2·D/3 + D/4, 1]];wxdraw2d( grid = true, color=blue, explicit(B1(1, 1,x), x, −1, 1), color=green, explicit(B2(1,1,x),x, −1, 1), color=black, explicit(B3(1,1,x),x, −1, 1), color=red, explicit(sommeB(1,1,x),x, −1, 1), color=orange, point_type=7, points(line) ); |

![(line) [[1/4,1],[7/12,1],[11/12,1]]](/dev/maxima/ferraris_htmlimg/ferraris_9.png)

(%i11) |
omega : 2·%pi·f; |
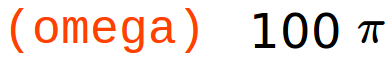
(%i12) |
A0 : 1; |

(%i15) |
A1(t) := A0·cos(omega·t); A2(t) := A0·cos(omega·t −2·%pi/3); A3(t) := A0·cos(omega·t −4·%pi/3); |
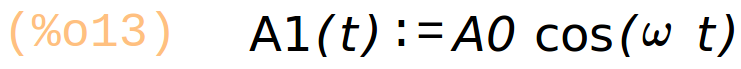
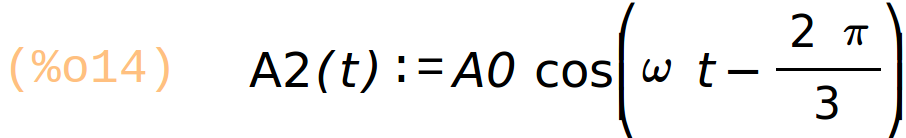
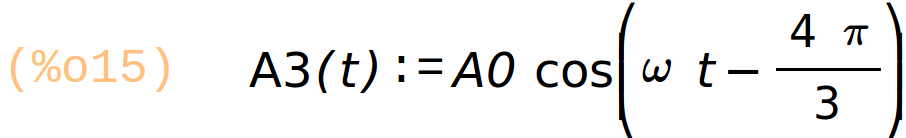
(%i18) |
champ1(x, t) := B1( A1(t), 1, x); champ2(x, t) := B2( A2(t), 1, x); champ3(x, t) := B3( A3(t), 1, x); |
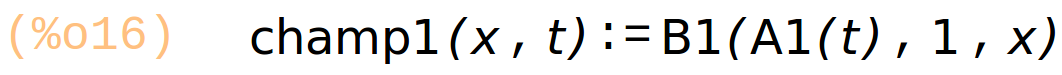
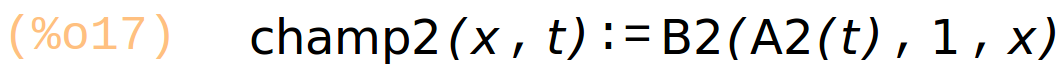
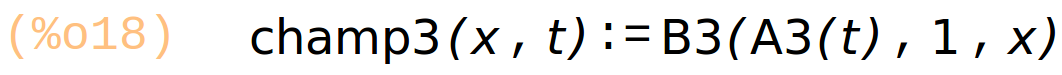
Traçage des 3 champs séparés, et de leur somme (en rouge).
(%i19) |
with_slider_draw(k, makelist(i·T/32, i, 0, 32), xrange=[0, 1], yrange=[−1.5, 1.5], xaxis = true, yaxis = true, color = blue, explicit(champ1(x, k),x,0,1), color = green, explicit(champ2(x, k),x,0,1), color = black, explicit(champ3(x, k),x,0,1), color=red, explicit( champ1(x, k)+champ2(x, k)+champ3(x, k) , x, 0, 1) ); |

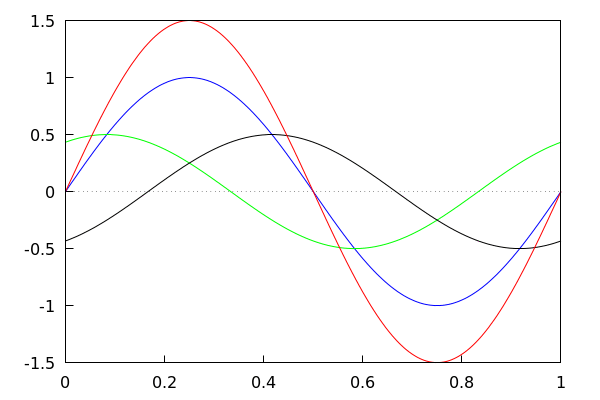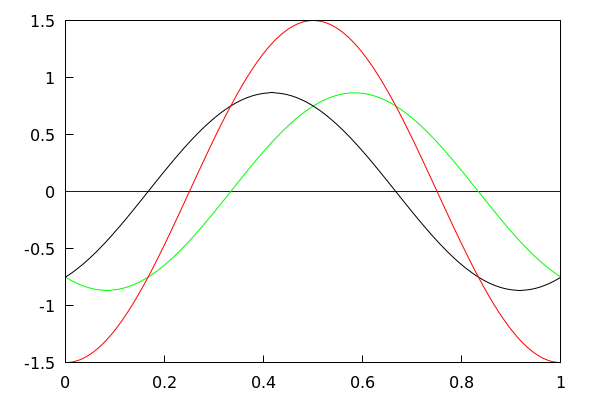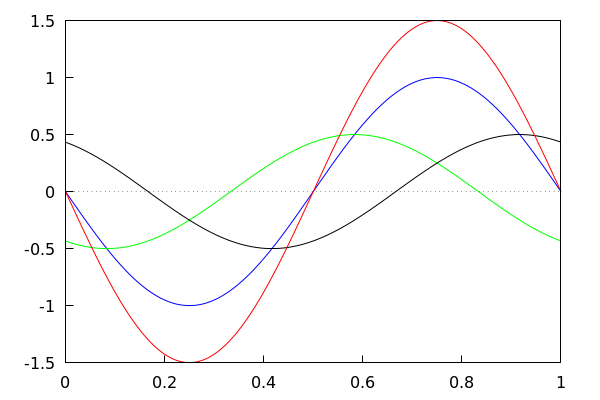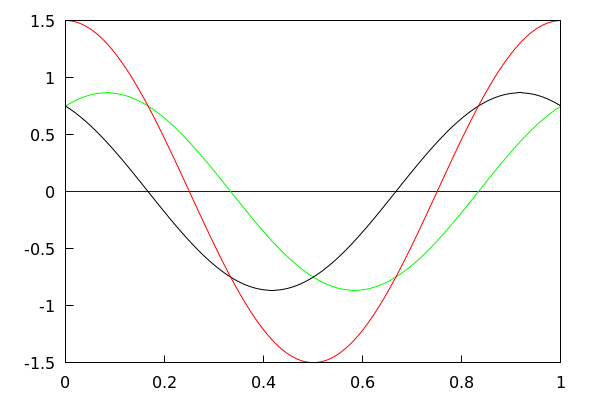
À faire :
- Voyez ce qui ce passe lorsqu’on inverse deux champs
par exemple, champ1(x, t) := B1( A2(t), 1, x);
et champ2(x, t) := B2( A1(t), 1, x); - Proposez un moteur à 2 phases.

Définition de la fonction en fragments :