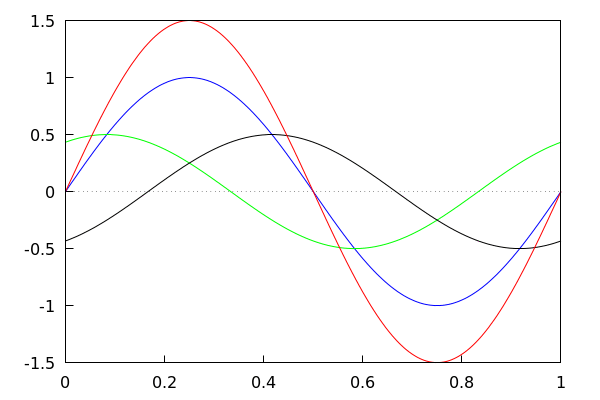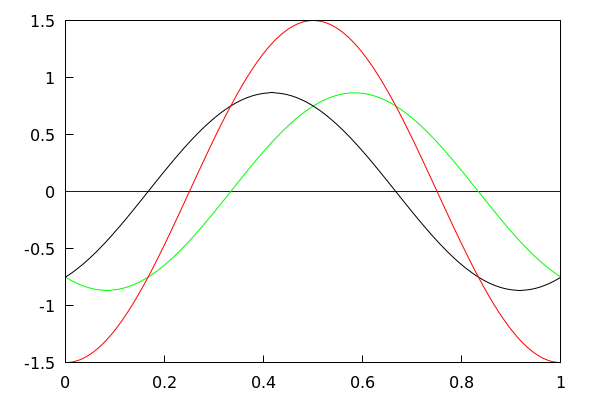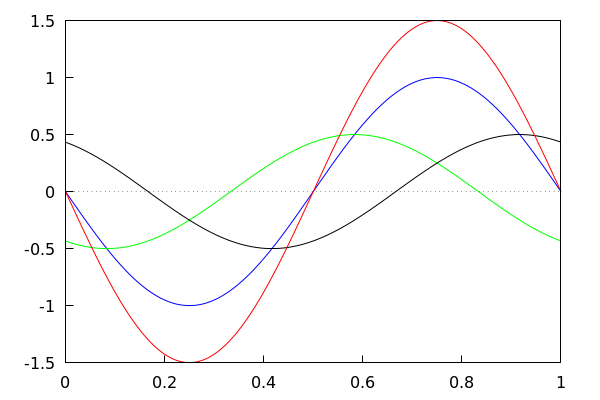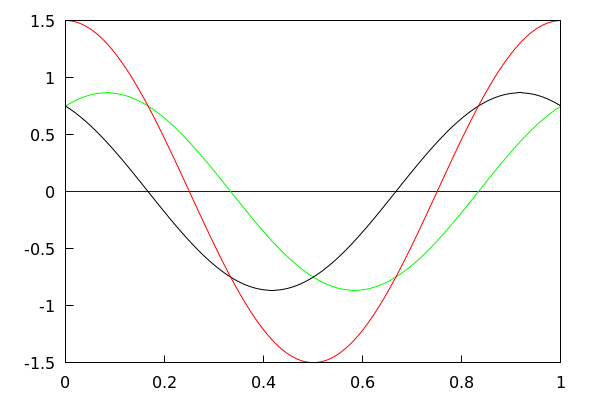
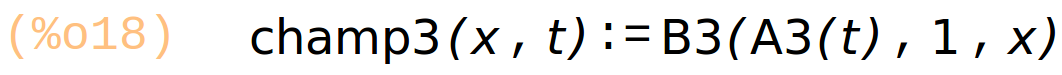Câblage
/**
* C.G. 2017 - Firmware ESP 8266-1 pour rObOscratch II
**/
#include <ESP8266WiFi.h>
#include <WiFiClient.h>
#include <ESP8266WebServer.h>
#include <ESP8266mDNS.h>
const char* ssid = "rObOtScratch";
const char* password = "56claude";
ESP8266WebServer server(80);
int bAV_D = 1; // variable d'état : moteur droite en avant (1) ou arrière (0)
int vAV_D = 0; // nb de ticks en position haute pour le hacheur
int vAV_Dold = 4; // pour reprendre à la meme vitesse apres un arret
int bAV_G = 1;
int vAV_G = 0;
int vAV_Gold = 4;
int h = 0;
void handleRoot() {
server.send(200, "text/plain", "CG 2017 PETIT ROBOT avec ESP8266");
}
void handleAV() {
bAV_D = 1;
vAV_D = vAV_Dold;
bAV_G = 1;
vAV_G = vAV_Gold;
}
void handleAR() {
bAV_D = 0;
vAV_D = vAV_Dold;
bAV_G = 0;
vAV_G = vAV_Gold;
}
void handleDR() {
bAV_D = 1;
vAV_D = vAV_Dold;
bAV_G = 0;
vAV_G = vAV_Gold;
}
void handleGA() {
bAV_D = 0;
vAV_D = vAV_Dold;
bAV_G = 1;
vAV_G = vAV_Gold;
}
void handlePlus() {
vAV_D++; if (vAV_D>10) vAV_D=10;
vAV_G++; if (vAV_G>10) vAV_G=10;
vAV_Dold = vAV_D;
vAV_Gold = vAV_G;
}
void handleMoins() {
vAV_D--; if (vAV_D<0) vAV_D=0;
vAV_G--; if (vAV_G<0) vAV_G=0;
vAV_Dold = vAV_D;
vAV_Gold = vAV_G;
}
void handleStop() {
vAV_Dold = vAV_D;
vAV_D = 0;
vAV_Gold = vAV_G;
vAV_G = 0;
}
void handleNotFound(){
String message = "File Not Found\n\n";
message += "URI: ";
message += server.uri();
message += "\nMethod: ";
message += (server.method() == HTTP_GET)?"GET":"POST";
message += "\nArguments: ";
message += server.args();
message += "\n";
for (uint8_t i=0; i<server.args(); i++){
message += " " + server.argName(i) + ": " + server.arg(i) + "\n";
}
server.send(404, "text/plain", message);
}
// HACHEUR
volatile int toggle;
void inline hacheur (void){
h++; if (h>10) h=0;
if (bAV_D == 1) { // moteur droite en avant
if (h < vAV_D) { digitalWrite(0, 1); digitalWrite(2, 0); }
else { digitalWrite(0, 0); digitalWrite(2, 0);}
} else {
if (h < vAV_D) { digitalWrite(0, 0); digitalWrite(2, 1);}
else { digitalWrite(0, 0); digitalWrite(2, 0);}
}
if (bAV_G == 1) { // moteur gauche en avant
if (h < vAV_G) { digitalWrite(1, 1); digitalWrite(3, 0);}
else { digitalWrite(1, 0); digitalWrite(3, 0);}
} else {
if (h < vAV_G) { digitalWrite(1, 0); digitalWrite(3, 1); }
else { digitalWrite(1, 0); digitalWrite(3, 0); } }
timer0_write(ESP.getCycleCount() + 80000);
// 80Mhz -> 80*10^6 = 1 seconde
// 80*10^3 = 1 ms
}
void setup(void){
int i = 0;
pinMode(0, OUTPUT);
pinMode(1, OUTPUT);
pinMode(2, OUTPUT);
pinMode(3, OUTPUT);
WiFi.begin(ssid, password);
delay(500);
// Attente de connexion
while (WiFi.status() != WL_CONNECTED) delay(500);
server.on("/", handleRoot);
server.on("/av",[](){handleAV(); server.send(200, "text/plain", "AV");});
server.on("/1", [](){server.send(200, "text/plain", "1");});
server.on("/0", [](){server.send(200, "text/plain", "0");});
server.on("/ar",[](){handleAR(); server.send(200, "text/plain", "AR");});
server.on("/dr",[](){handleDR(); server.send(200, "text/plain", "DR");});
server.on("/ga",[](){handleGA(); server.send(200, "text/plain", "GA");});
server.on("/+", [](){handlePlus(); server.send(200, "text/plain", "+");});
server.on("/-", [](){handleMoins(); server.send(200, "text/plain", "-");});
server.on("/st",[](){handleStop(); server.send(200, "text/plain", "STOP");});
server.onNotFound(handleNotFound);
server.begin();
noInterrupts();
timer0_isr_init();
timer0_attachInterrupt(hacheur);
timer0_write(ESP.getCycleCount() + 80000000);
interrupts();
}
void loop(void){
server.handleClient();
}




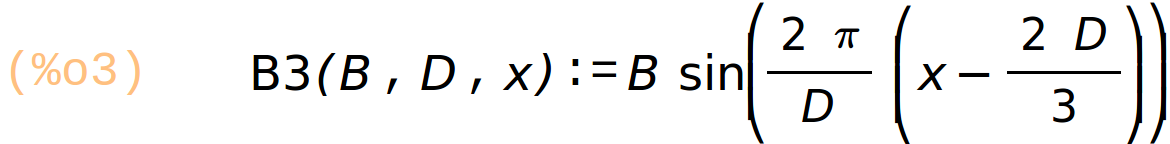
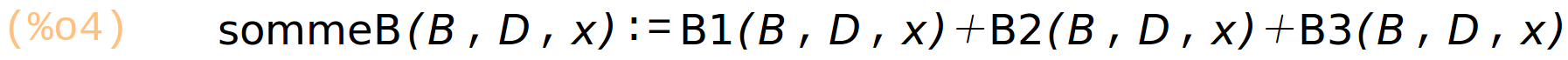



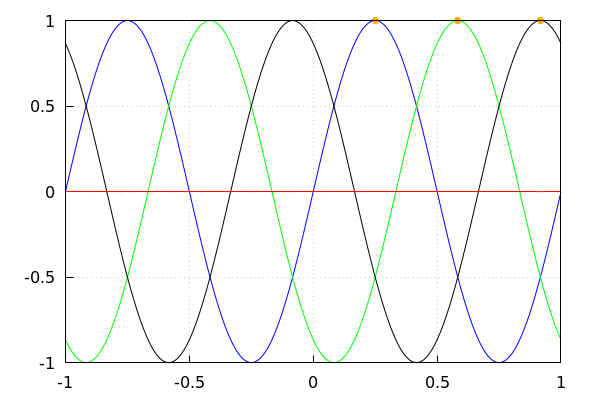
![(line) [[1/4,1],[7/12,1],[11/12,1]]](/dev/maxima/ferraris_htmlimg/ferraris_9.png)